속도 < 방향
Dynamical Isometry and a Mean Field Theory of CNNs:How to Train 10,000-Layer Vanilla Convolutional Neural Networks 논문 리뷰와 Summary 본문
Dynamical Isometry and a Mean Field Theory of CNNs:How to Train 10,000-Layer Vanilla Convolutional Neural Networks 논문 리뷰와 Summary
import max 2022. 1. 28. 10:23[업데이트 : 2022-01-30]
2018년에 발표된
Dynamical Isometry and a Mean Field Theory of CNNs:How to Train 10,000-Layer Vanilla Convolutional Neural Networks
논문의 Summary 겸 리뷰를 적어보려고 합니다.
글을 쓰기에 앞서, 공부를 위해 논문을 보며 요약, 작성한 내용이라 간혹 오역이나 잘못된 내용이 있을 수 있습니다.
핵심 키워드는 highlight를 해두었습니다. 틀린 부분은 댓글로 알려주시면 감사하겠습니다^^
편의상 경어체를 빼고 작성합니다.
Abstract
우리는 신호 전파(propagation)에 대한 평균 필드 이론(mean field theory)을 개발하고 입력-출력 야코비안(Jacobian) 행렬의 특이값의 평형인 동적 등각도(dynamic isometry) 에 대한 조건을 특성화하여 이 초기화 방식을 이론적으로 유도한다.

Introduction
Deep CNN은 딥러닝의 성공에 매우 중요했으며 이를 기반으로 한 아키텍처는 컴퓨터 비전, 음성인식, NLP, 그리고 바둑(알파고)까지 뛰어난 정확도를 달성했다. Deep CNN의 성능은 네트워크가 더 깊어짐에 따라 향상되었으며, 일부 모델은 수백~수천 개의 레이어를 사용했다. 그러나 너무 깊은 아키텍처는 잔여(residual) 연결이나 배치 정규화같은 기술과 사용해야만 훈련할 수 있다.
최근 연구에서는 평균 필드 이론(mean field theory)를 사용하여 랜덤 매개변수가 있는 신경망에 대한 이론적 이해를 구축했다. 이러한 연구는 초기화 시 신호가 전파될 수 있는 최대 깊이를 밝혀냈고, 신호가 모든 경로를 통과할 때 네트워크가 정확하게 학습될 수 있음을 확인했다.
Fully-connected layer의 초기화 하이퍼파라미터 공간에서 순서대로 정렬됨을 추가적으로 예측할 수 있다. 평균 필드 이론은 "평균"을 포착하지만 경사 하강의 안정성에 중요한 변동의 규모를 정량화하지 않는다.
입출력에서 랜덤 행렬을 사용하여 활성화 함수와 특이값의 분포를 정량화했다. 초기 무작위 가중치 행렬이 그려지는데, 야코비안(Jacobian) 행렬이 잘 조절될 때 네트워크가 가장 효율적으로 훈련될 수 있다. 이미지가 작은 경우에도 채널수가 많다는 한계에서 잘 정의된 평균 필드 이론이 심층신경망에 존대한다는 걸 알 수 있다. 심층 신경망은 Fully-connected layer와 정확히 동일한 순서를 가지며 정렬 단계에서 gradient-vanishing 문제, 그리고 chaos 단계에서 gradient exploding 문제가 발생한다는 것을 알 수 있다. 또한 Fully-connected layer와 마찬가지로 임계값에서 초기화되는 매우 깊은 CNN이 두 단계를 분리하는 것은 상대적으로 쉽게 훈련될 수 있다.
또한 랜덤 행렬(random matrix) 에 대한 분석이 convolution으로 이어지는데, block-circulant 구조가 야코비안 행렬이 신경망 속에서 fine tuning을 할 때 간편하게 할 수 있다. 이 초기화를 사용함으로서 일반적인 컨볼루션 모델보다 훨씬 빠르게 학습할 수 있다.
Fully-connected layer와 심층 신경망의 order-to-chaos는 동일해보이지만, 평균 필드 이론(mean field theory)는 사실 상당히 다르다는 점을 강조한다. 깊은 깊이의 한계에서 신호는 최소한의 공간 구조로 모드를 전파할 수 있다. Delta-orthogonal 초기화에서 orthogonal 커널은 균일하지 않은 분포에서 추출되며 성능 저하 없이 10,000개 이상의 레이어로 구성된 바닐라 CNN을 학습할 수 있다.
Theoretical results
랜덤 컨볼루션 신경망에서 신호 전파에 대한 평균 필드 이론을 도출할 것이다. 일반적인 방법론을 따르면 야코비안(Jacobian) 행렬의 특이값 분포에 대한 이론에 도달하게 된다. 이 커널은 합성곱 신경망의 motivation을 유도할 수 있도록 해주고, 이러한 커널이 바닐라 CNN에 대한 기존 초기화 방식보다 성능이 좋다는 것을 알 수 있다.
2.1 A mean field theory for CNNs
2.1.1 RECURSION RELATION FOR COVARIANCE
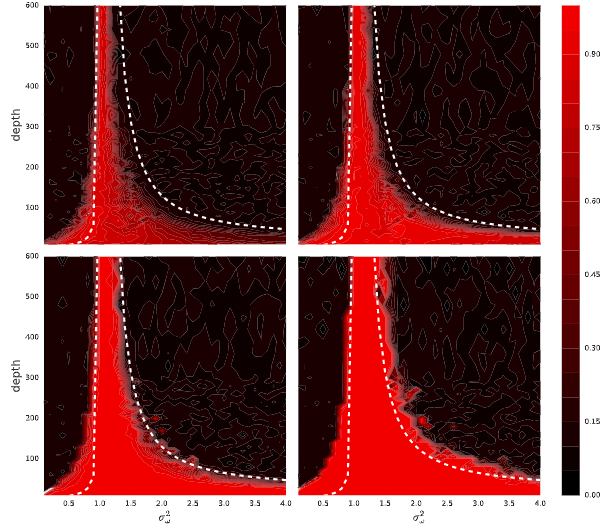
평균 필드 이론은 CNN의 최대 훈련 가능한 깊이를 예측하기 때문에 분산 값이 위와 같은 경우 히트맵은 가중치 분산에 따라 특정 값에 수렴을 하며 깊이의 배수에 따라 달라짐을 알 수 있다.

다양한 깊이의 CNN 중 orthogonal 커널을 사용한 곡선들은 결과적으로 accuracy가 100%에 도달하지만 그렇지 않고 일반적인 초기화를 사용한 곡선들은 깊이가 증가함에 따라 성능이 저하됨을 알 수 있다. 따라서 Delta-orthogonal 초기화는 깊이가 증가함에 따라 테스트 성능이 감소하는 문제를 해결한다.
Discussion
CNN에서 신호가 전파될 때 평균 필드 이론에 기반하여 전파되는 연구를 진행했고, 신호가 네트워크를 통해 앞뒤로 흐르기 위한 필요 조건을 연구함으로써 바닐라 CNN의 훈련을 쉽게 훈련하는 초기화 방식을 발견했다.
연구에서 제시한 방법은 동적 등각도(dynamic isometry)이며 즉, 야코비안(Jacobian) 행렬의 네트워크 입출력을 활성화할 때, 랜덤 orthogonal 커널을 생성하여 초기화할 수 있도록 진행했다. Fully-connected layer와 반대로 CNN의 신호는 다차원이다. 이번 연구에서는 이 신호를 푸리에 모드로 분해하는 방법과 신호 전반에 걸쳐 전파를 촉진하는 것을 연구했고, 10,000개 이상의 레이어로 기본 CNN을 훈련하는 것이 가능하다는 것을 발견했다.
위의 행위를 통해 무작위로 vanilla CNN을 훈련할 때 발생하는 모든 장애물을 제거했으며, 딥러닝 커뮤니티에서 나오는 깊이만으로 성능을 향상시킬 수 있는지에 대한 질문를 다룰 수 있기 위한 토대를 마련했다. 초기 결과는 수십~수백 개의 레이어오 특정 깊이를 지나면 vanilla CNN의 아키텍쳐의 성능이 포화되는 것으로 나타났다.
이를 통해 residual 연결이나 배치 정규화같은 기능이 단순히 '학습을 효율적으로 하는 것'보다 '좋은 모델 클래스를 정의하는 것'에 중요한 역할을 할 가능성이 있다는 점을 시사할 수 있다.




