속도 < 방향
Forecasting : 예측이란? 예측에 대한 기초 본문
Forecasting : Principles and Practice 온라인 교재를 보며 참고하였습니다.
Chapter 1.
우리는 많은 경우에 예측을 한다. 비단 현대사회뿐만 아니라 수천년전부터 사람들은 예측을 하는 것에 관심이 많았다. 고대 바빌로니아의 예측가는 썩은 양의 간에서 구더기의 분포를 미래를 예언하기도 했다. 이처럼, 계획을 세우는 데 있어 예측은 큰 도움이 된다. 예측가능성은 다음과 같은 요인에 의존하게 된다.
- 영향을 주는 요인을 얼마나 잘 이해할 수 있는지
- 사용할 수 있는 데이터가 얼마나 많은지
- 예측이 우리가 예측하려는 것에 영향을 줄 수 있는지 여부
전기 수요 예측의 경우는 위의 조건이 모두 맞기 때문에 상당히 정확한 편이다. 하지만, 환율 예측의 경우에는 2번의 조건만 만족하기 때문에 예측이 정확하지 않은 경우도 있다. 예를 들어 환율 예측은 환율 자체에 직접적으로 영향을 주기도 한다. 즉, 예측 자체 때문에 예측이 맞는 상황이 되기도 하는 것이다. 이러한 상황을 '효율적인 시장 가설(efficient market hypothesis)' 라고 볼 수 있다.
좋은 예측이란 과거 데이터에서 존재하는 진짜 패턴과 관계를 잡아낸다. 환경이 변하는 경우에 예측이 불가능할 것이라고 대부분 생각한다. 하지만 모든 환경은 변화고, 좋은 예측 모델이랑 변하는 '방식'을 잡아내는 것이다. 즉, 환경이 변하는 방식이 미래에도 계속될 것이라는 가정 하에 예측을 하는 것이다.
1.2 예측, 계획 그리고 목표
예측은 경영을 함에 있어 큰 도움을 줄 수 있는 업무이다. 상세하게 보면 크게 세 분류로 나눠 정의해 볼 수 있다.
- 예측(Forecasting) : 주어진 이용가능한 모든 정보를 바탕으로 가능한 한 정확하게 미래를 예측하는 것
- 목표(Goals) : 발생하길 기대하는 희망사항. 목표가 실현 가능한지에 대한 예측 없이 목표를 세우는 경우도 있다.
- 계획(Planning) : 예측과 목표에 대한 대응. 예측과 목표를 일치시키는 데 필요한 행동을 결정하는 일을 포함한다.
예측은 용도 및 기간에 따라 세 분류로 나눠볼 수 있다.
- 단기 예측 : 인사, 생산, 수송 계획, 수요 예측
- 중기 예측 : 원자재 구입, 신규 채용, 장비나 기계 구입
- 장기 예측 : 보통 전략적으로 계획을 세우는 데 사용한다. 시장 기회, 환경 요인, 내부 자원을 반드시 고려해야 한다.
1.3 어떤 것을 예측할 지 결정하기
예측 프로젝트의 초기 단계에서는 어떤 것을 예측할지 결정해야 한다. 예를 들어 생산 환경에서 물품에 대한 예측이 필요하다면,
- 모든 생산 라인에 대한 것인가? 혹은 생산 그룹에 대한 것인가?
- 모든 판매점에 대한 것인가? 지역별 판매점 그룹에 대한 것인가? 전체 판매량에 대한 것인가?
- 주별 데이터인가? 월별 데이터인가? 연간 데이터인가?
등을 고려해야 할 것이다. 예측 범위, 예측 빈도도 고려해야 한다. 또한 예측값을 만들기 전, 예측값을 사용할 사람과 대화하며 사용자의 필요에 대한 이해도 필요할 것이다. 앞의 과정이 이뤄지고 나서야 예측에 필요한 데이터를 찾아야 한다. 예측을 하는 사람이 가장 시간을 많이 쏟는 부분은 데이터를 찾고 모아서 분석하는 부분이다.
1.4 예측 데이터와 기법
어떤 데이터를 사용할 수 있는지에 따라 예측 기법이 달라진다. 만약 이용할 수 있는 데이터가 없거나, 이용할 수는 있지만 예측에 상관 없는 데이터라면, 정량적인 예측 기법(Quantitive Forecasting)을 사용해야 한다.
- 과거 수치 정보를 사용할 수 있을 때
- 과거 패턴의 몇 가지 양상이 미래에도 계속될 것이라고 가정하는 것이 합리적일 때
위의 두 가지 조건을 만족할 때 정량적인 예측을 사용할 수 있으며 여러 정량적 예측 기법이 있다. 대부분 정량적 예측 문제는 일정한 간격으로 모은 시계열 (LSTM) 데이터나 특정 시점에서 모은 횡단면(cross-sectional) 데이터를 사용한다.
시계열 예측
- IBM 일별 주가
- 월별 강우량
- Amazon의 분기별 판매 결과
- Google의 연간 수익
위와 같이 시간에 따라 순차적으로 관측된 데이터를 시계열로 다룰 수 있다. 시계열을 예측할 때, 목표는 관측값이 미래에 계속될 것인지 예측하는 것이다.

호주 맥주의 분기별 생산량이며, 파란색 부분은 다음 2년에 대한 예측값이다. 예측값들이 과거 데이터에서의 패턴을 얼마나 잘 캐치하고 다음 2년에 대해 잘 모사하는지 주목해서 봐야 한다.
어둡게 그늘로 표시한 영역은 80% 예측 구간(prediction interval)을 의미한다. 즉, 미래값이 80%의 확률로 어두운 그늘로 표기한 영역에 들어갈 것으로 예측하는 것이다. 밝은 그늘로 표시한 영역은 95% 예측 구간을 의미한다. 이러한 예측 구간은 예측의 불확실성을 나타낼 때 유용하다.
가장 단순한 시계열 예측 기법은 예측할 변수 정보만 이용하고, 변수의 행동에 영향을 미치는 다른 요인들은 고려하지 않는다. 시계열 예측용 모델에는 분해모델 (decomposition models), 지수평활 (exponential smoothing models) ,ARIMA 모델 등이 있다.
예측 변수와 시계열 예측
예측 변수는 시계열을 예측할 때 유용하다. 예를 들어 여름 동안 더운 지역의 시간당 전기 수요(ED, electricity demand)를 예측한다면 예측 변수를 고려해야할 것이다.

현재 기온, 경제 상황, 인구, 시간, 요일, 오차 중 어떤 것이 전기 수요의 변동을 일으키는지 설명할 때 도움이 되기 때문에 이 모델을 설명 모델(explanatory model)이라고 부른다.
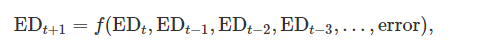
여기에서 설계한 모델의 t는 현재시간, t-1은 한 시간 전, t+1은 한 시간 후로 변수의 과거 값으로 미래 예측을 한다.

위의 두 모델의 특징을 결합한다면 위와 같이 혼합된 모델링을 할 수 있다. 이러한 모델은 동적 회귀 (dynamic regression) 모델, 패널 데이터(panel data) 모델, 종단(longtudinanl) 모델, 수송 함수(transfer function) 모델, 선형 시스템(linear system) 모델 등 다양한 종류의 모델이 있다.
이러한 모델들은 변수의 과거 값만 다루지 않고 다른 변수에 대한 정보도 포함하기 때문에 유용하게 사용할 수 있다. 하지만 설명 모델이나 혼합된 모델 대신에 시계열 모델을 선택할 수도 있는 다양한 경우가 있다.
- 변수의 행동에 영향을 주는 관계를 측정하기가 어려운 경우
- 관심 있는 변수를 예측하려면 다양한 예측 변수의 미래값을 알 필요가 있거나 예측할 필요가 있는 경우
- 주된 관심이 '왜' 일어나는지가 아니라 '무엇'이 일어나는지에 있는 경우
이처럼 데이터나 모델의 정확도, 사용될 방식에 따라 예측에 사용할 모델이 달라진다.
1.6 예측 작업의 기본 단계
- 문제 정의
- 정보 수집
- 예비 분석
- 모델 선택 및
- 예측 모델 사용 및 평가
1.7 통계적 예측 관점
예측값은 확률 변수(random variable)가 비교적 높은 확률로 취할 수 있는 값들의 범위를 제시하는 예측 구간(prediction interval)을 수반한다.
우리가 아는 A 라는 값이 주어진 상황에서의 무작위 변수가 가질 수 있는 값은 확률 분포(probability distribution) 라고 하며, 예측을 함께 제시했을 때 예측분포(forecast distribution)라 한다.
'예측'을 말할 때 보통은 예측 분포의 평균을 가리킨다.
'개발 > Data Science' 카테고리의 다른 글
| [시계열] 시계열의 개요와 역사 (0) | 2022.09.14 |
|---|---|
| Forecasting : 시계열 회귀 모델(수정중) (0) | 2022.02.24 |
| Forecasting : 판단 예측 (0) | 2022.02.19 |
| Forecasting : 예측가의 도구 상자 (0) | 2022.02.12 |
| Forecasting : 시계열 시각화 (0) | 2022.02.03 |




