속도 < 방향
Forecasting : 예측가의 도구 상자 본문
Forecasting : Principles and Practice 온라인 교재를 보며 참고하였습니다.
Chapter 3.
예측을 하는 데 있어 유용한 도구들과 예측 작업을 단순하게 만드는 법, 예측 기법에서 이용 가능한 정보를 적절하게 사용하게 사용했는지 확인하는 법, 예측구간(prediction interval)을 계산하는 기법 등을 살펴볼 것이다.
3.1 몇 가지 단순한 예측 기법
평균 기법
예측한 모든 미래의 값은 과거 데이터의 평균과 같다. 과거 데이터를 y1,…,yT라고 쓴다면, 예측값을 다음과 같이 쓸 수 있다.

meanf(y, h)
# 시계열, 예측범위
단순 기법(naïve method)
단순 기법에서는 모든 예측값을 단순하게 마지막 값으로 둔다. 이 기법은 금융 시계열을 다룰 때 잘 들어맞는다.

naive(y, h)
rwf(y, h) # 위의 것과 같은 역할을 하는 함수데이터가 확률보행(random walk) 패턴을 따를 때는 단순 기법(naïve method)이 최적이라서 확률보행 예측값(random walk forecasts)이라고 부르기도 한다.
계절성 단순 기법(Seasonal naïve method)
계절성이 아주 뚜렷한 데이터를 다룰 때 비슷한 기법이 유용하다. 이 기법에서는 각 예측값을 연도의 같은 계절의(예를 들면, 이전 연도의 같은 달) 마지막 관측값으로 둔다. T+h에 대한 예측을 식으로 쓰면,
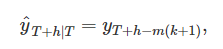
m은 계절성의 주기(seasonal period), k=⌊(h−1)/m⌋+1, ⌊u⌋은 u의 정수 부분을 나타낸다. 식으로 쓰니 실제 내용보다 복잡해 보이는데, 예를 들면 월별 데이터에서 미래의 모든 2월 값들의 예측값이 마지막으로 관측한 2월 값과 같다. 분기별 데이터에서, 미래의 모든 2분기 값의 예측치가 마지막으로 관측한 2분기 값과 같다. 다른 달과 분기, 다른 계절성 주기에 대해 같은 방식으로 적용할 수 있다.
표류 기법
단순 기법(naïve method)을 수정하여 예측값이 시간에 따라 증가하거나 감소하게 할 수 있다. 여기에서 (표류(drift)라고 부르는) 시간에 따른 변화량을 과거 데이터에 나타나는 평균 변화량으로 정한다. 그러면 T+h 시간에 대한 예측값은 다음과 같이 주어진다.

처음과 마지막 관측값에 선을 긋고 이 선을 외삽(extrapolation)한 것과 같다.
rwf(y, h, drift=TRUE)
# Set training data from 1992 to 2007
beer2 <- window(ausbeer,start=1992,end=c(2007,4))
# Plot some forecasts
autoplot(beer2) +
autolayer(meanf(beer2, h=11),
series="평균", PI=FALSE) +
autolayer(naive(beer2, h=11),
series="단순", PI=FALSE) +
autolayer(snaive(beer2, h=11),
series="계절성 단순", PI=FALSE) +
ggtitle("분기별 맥주 생산량 예측값") +
xlab("연도") + ylab("단위: 백만 리터") +
guides(colour=guide_legend(title="예측"))
1992년부터 2007년까지의 맥주 생산량을 세 가지 기법을 통해 예측한 값이다.
# Plot some forecasts
autoplot(goog200) +
autolayer(meanf(goog200, h=40),
series="평균", PI=FALSE) +
autolayer(rwf(goog200, h=40),
series="나이브", PI=FALSE) +
autolayer(rwf(goog200, drift=TRUE, h=40),
series="표류", PI=FALSE) +
ggtitle("구글 주식 (2013년 12월 6일까지)") +
xlab("날짜") + ylab("종가(미국 달러)") +
guides(colour=guide_legend(title="예측"))
구글의 200일간의 주식 종가를 기초로 예측한 값이다.
이런 단순한 기법이 가장 좋은 예측 기법이 될 수 있다. 하지만 대부분, 이러한 기법은 다른 기법보다는 벤치마크 역할을 할 것이다.
3.2 변환과 조정
과거 데이터를 조정하면 예측 작업이 더 쉬워진다. 여기에서 달력 조정, 인구 조정, 인플레이션 조정, 수학적 변환 등 이렇게 4종류의 조정 방식을 다룬다. 이러한 변환과 조정 방식을 사용하는 목적은 변동의 알려진 원인을 제거하거나 전체 데이터 모음에 걸친 패턴을 더 일관성 있게 만들어서 과거 데이터에 나타나는 패턴을 단순하게 만드는 것이다.
달력 조정
계절성 데이터에 나타나는 변동은 단순히 달력 때문일 수 있다. 이럴 땐, 예측 모델을 피팅하기 전에 변동을 제거해 볼 수 있다. monthdays() 함수로 각 월과 각 분기의 날짜를 계산할 수 있다.
dframe <- cbind(Monthly = milk,
DailyAverage = milk/monthdays(milk))
colnames(dframe) <- c("월별", "일별 평균")
autoplot(dframe, facet = TRUE) +
xlab("연도") + ylab("파운드") +
ggtitle("젖소별 우유 생산량")
월별 데이터와 일별 데이터를 비교해보면 일별 데이터가 더 단순한 것을 알 수 있다. 그 이유는 월 길이가 매월 다르다는 변동을 제거하고 일별 평균 생산량을 봤기 때문이다.
인구 조정
인구 변화에 영향을 받는 데이터를 1명당 데이터로 조정할 수 있다. 즉, 전체 대신에 1명당 데이터(또는 천명, 백만명)를 고려하는 것이다. 예를 들어, 어떤 특정 지역에서 시간에 따른 병원 침상 개수를 다루고 있다고 했을 때, 1,000명당 침상수를 고려하여 인구 변화 효과를 제거하면, 결과를 해석하기가 훨씬 더 쉬워진다. 그러면 침상 수가 정말로 증가했는지 여부나 증가량이 완전히 인구 증가에 따른 자연스러운 현상인지 여부를 확인할 수 있다. 전체 침상 수는 증가하지만 천명당 침상수는 감소할 수도 있다. 인구가 병원 침상수보다 빠르게 증가하면 이런 현상이 나타난다. 인구 변화에 영향을 받는 대부분의 데이터에서 전체보다 1명당 데이터를 다루는 것이 좋다.
인플레이션 조정
돈의 가치에 영향을 받는 데이터는 모델링에 앞서 적절하게 조정되어야 한다. 예를 들면, 인플레이션 때문에 이전 몇 십년 동안 새로운 집의 평균 가격이 증가했을 것이다. 올해 $200,000 가격의 집은 20년 전 $200,000 가격의 집과 같지 않다. 이러한 이유에서, 보통은 모든 값을 특정 연도의 달러 가치로 나타내도록 금융 시계열을 조정한다. 예를 들면, 주택 가격 데이터는 2000년대의 달러로 나타낼 수 있다. 이렇게 조정하기 위해, 가격 지수를 사용한다. 종종 정부 기관에서 가격 지수를 만든다. 소비재에 대해, 보통 가격 지수는 소비자 가격 지수(또는 CPI)다.
수학적 변환
데이터에서 시계열의 수준에 비례하여 증가/감소하는 변동이 보이면, 변환(transformation)이 유용할 수 있다. 예를 들면, 로그 변환(log transformation)이 유용하다. 로그의 밑을 10으로 사용하면, 로그 눈금에서 1만큼 증가하는 것이 원래의 눈금에서 10배 증가한 것과 대응된다. 로그 변환의 또 다른 장점은 원래의 눈금에 대해 예측치를 그대로 양수로 놓는다는 점이다.
제곱근(루트)과 세제곱근을 사용할 수 있다. 이것은 거듭곱 변환(power transformation)이라고 한다.
로그 변환과 거듭곱 변환을 둘 다 포함하는 유용한 변환은 박스-칵스(Box-Cox) 변환의 일종이다. 박스-칵스(Box-Cox) 변환은 매개변수 λ에 따라 달라지고 다음과 같이 정의됩니다.
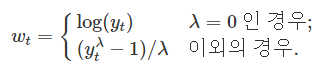
박스-칵스(Box-Cox) 변환에서 로그는 항상 자연 로그다. 그래서 λ=0이면, 자연 로그를 사용하지만, λ≠0이면, 거듭곱 변환(power transformation)을 사용한다. λ=1이면, wt=yt−1이라, 변환된 데이터에서 시계열의 모양 변화 없이 아래쪽으로 이동하게 된다. 하지만, 모든 다른 값에 대해서는, 시계열의 모양이 변할 것이다.
(lambda <- BoxCox.lambda(elec))
#> [1] 0.2654
autoplot(BoxCox(elec,lambda))BoxCox.lambda() 함수를 통해 필요한 값을 선택할 수 있다.
거듭곱 변환의 특징
- 어떤 yt≤0에서는 모든 관측값에 어떤 상수를 더해서 조정하지 않으면 거듭곱 변환을 사용할 수 없다.
- 단순한 값을 선택하면 설명하기 더 쉬워진다.
- 예측 결과가 상대적으로 값에 따라 민감하게 변하지는 않는다.
- 종종 변환이 필요 없을 수 있다.
- 변환해도 예측값에는 때때로 거의 차이가 없지만, 예측구간(prediction interval)에는 커다란 영향을 준다.
편향조정
역-변환된 점예측값(point forecast)이 예측 분포의 평균이 되지 않는다. 평균은 합산 과정이지만, 중간값(median)은 그렇지 않다. 로그 변환(log transform)은 예측값과 예측 구간이 반드시 양수가 되도록 하는 데 쓸모가 있다.
주어진 평균 사이의 차이를 편향(bias)이라고 부른다. 중간값 대신 평균을 사용할 때, 점 예측치들이 편향-조정(bias-adjustment)되었다고 말한다.
'개발 > Data Science' 카테고리의 다른 글
| [시계열] 시계열의 개요와 역사 (0) | 2022.09.14 |
|---|---|
| Forecasting : 시계열 회귀 모델(수정중) (0) | 2022.02.24 |
| Forecasting : 판단 예측 (0) | 2022.02.19 |
| Forecasting : 시계열 시각화 (0) | 2022.02.03 |
| Forecasting : 예측이란? 예측에 대한 기초 (0) | 2022.01.28 |




