속도 < 방향
Forecasting : 시계열 시각화 본문
Forecasting : Principles and Practice 온라인 교재를 보며 참고하였습니다.
Chapter 2.
데이터 분석 작업에서 가장 먼저, 많이 하는 것이 데이터 시각화다. 그래프를 통해 패턴, 관측값, 변수에 따른 변화, 변수 사이의 관계 등 데이터의 많은 특성을 파악할 수 있다. 데이터 시각화 과정은 예측 기법에 반드시 포함되어야 한다.
2.1 ts객체
시계열이란 각 숫자가 기록된 시간에 관한 정보가 있는 숫자들의 목록이다. R에서는 이러한 정보를 ts 객체로 저장할 수 있다.
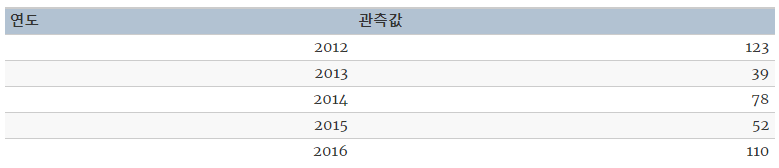
y <- ts(c(123,39,78,52,110), start = 2012)위와 같은 관측값의 데이터를 활용하여 예측할 때는, ts() 메서드를 활용하여 ts 객체로 바꿀 수 있다.
y <- ts(z, start = 2003, frequency = 12)만약 자주 관측된 값의 경우라면 단순하게 frequency 입력값만 추가하면 된다. 월별 데이터가 수치 벡터 z에 저장되어 있는 것 또한 ts 객체로 바꿀 수 있다.
시계열의 빈도
빈도(frequency) 는 특정 구간의 패턴(계절성)이 반복되기 전까지의 관측값의 수를 의미한다. 물리학이나 푸리에(Fourier) 분석에서는 이것을 '주기(period)'라고 부른다.

실제로 1년은 52주가 아니고 윤년이 있기 때문에 평균적으로 52.18 주임을 알 수 있다. 하지만 ts() 객체는 입력값이 정수여야 한다. 관측값의 빈도가 주 1회 이상일 때는 주간/연간/시간별/일별 등 다양한 기간 동안의 계절성이 있을텐데 그 중 어떤 항목이 중요도가 높은지에 따라 결정해야 할 것이다.
2.2 시간 그래프
시계열 데이터에서 가장 먼저 그려야 할 요소는 시간 그래프(time plot) 이다. 즉, 관측값을 관측 시간에 따라 인접한 관측값을 직선으로 연결하여 그리는 것이다.
autoplot(melsyd[,"Economy.Class"]) +
ggtitle("Economy passengers : melbourne - sydney") +
xlab("year") +
ylab("passenger(unit:1000person)")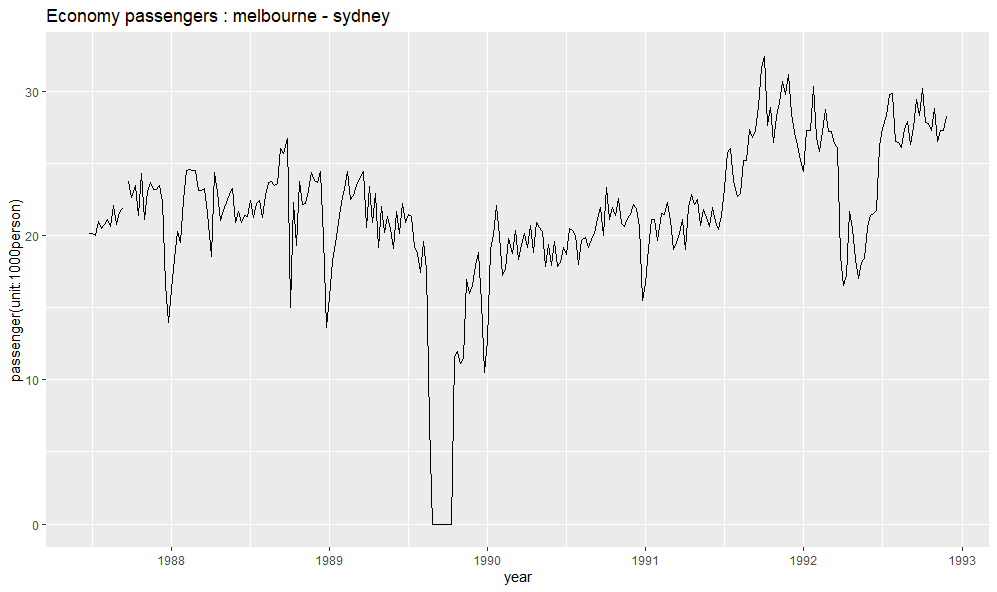
autoplot() 메소드를 활용해 그래프를 그릴 수 있다. 미래 승객수를 예측하기 위해 위의 그래프에서 발견할 수 있는 특징 전부를 모델링에서 고려해야 한다.
autoplot(a10) +
ggtitle("Antidiabetic drug sales") +
ylab("$ Millionr") +
xlab("Year")
당뇨병 약의 매출을 확인했는데, 시계열의 수준이 증가함에 따라 계절성 패턴의 크기 또한 증가하는 것을 알 수 있다. 또한 연초마다 매출이 급감하는 이유는 정부의 보조금 정책 때문이다. 이 시계열을 활용한 예측에서는 위의 계절성 패턴과 더불어 변화의 추세가 느리다는 사실을 예측치 안에도 담아내야 한다.
2.3 시계열 패턴
● 추세(trend) : 데이터가 장기적으로 증가/감소할 때 존재하는 패턴이나 방향성. 추세는 선형적일 필요는 없다. 예를 들어 추세가 '증가'에서 '감소'로 변할 때, '추세의 방향이 변했다' 라고 언급할 수 있다.
● 계절성(seasonality) : 해마다 어떤 특정한 때나 1주일마다 특정 요일에 나타나는 등의 요인. 보통 빈도의 형태로 나타나는데, 그 빈도는 항상 일정하다.
● 주기성(cycle) : 고정된 빈도 가 아닌 형태로 증가나 감소하는 모습을 보일 때 주기(cycle)가 나타난다. 보통 경제 상황이나 '경기 순환(business cycle)' 때문에 일어나는 경우가 있다. 이런 변동성의 지속기간은 적어도 2년 이상 나타난다.
많은 사람들이 주기성(cycle)과 계절적인 패턴(seasonality)을 혼동하지만 둘은 굉장히 다르다. 일정하지 않다면 주기성이고, 빈도가 일정하고 특정 시기와 연관이 있다면 계절성이다. 일반적으로 주기성은 계절성의 패턴보다 길고 변동성도 큰 편이다.
2.4 계절성 그래프
● 계절성 그래프는 각 계절에 대해 관측한 데이터를 나타낸다는 점을 제외하고 시간 그래프와 비슷하다.
library(forecast)
ggseasonplot(a10, year.labels = TRUE, year.labels.left = TRUE) +
ylab("$ Million") +
xlab("Month") +
ggtitle("Seasonal Graph : Antidibiatic drug sales")seasonplot() 을 사용하면 계절적인 변동이 있는 데이터를 그리기에 좋다. seasonplot은 forecast 패키지에 들어있기 때문에 libarary(forecast)를 통해 먼저 설치를 하고 메서드를 실행하면 아래와 같은 그래표를 확인할 수 있다.
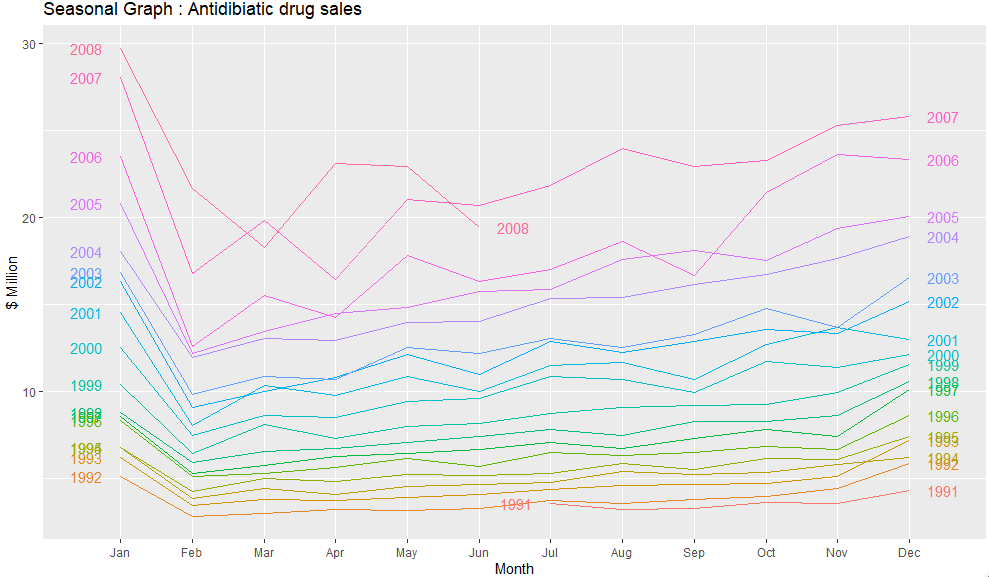
2.2 에서 다뤘던 데이터와 같은 데이터지만 데이터를 계절별로 포개며 나타내고 있다. 중요한 계절성 패턴을 시각적으로 분명하게 보여주고 있다. 특히, 매년 1월에 매출이 크게 뛰는데, 소비자들이 연말에 당뇨병 약을 사재기하는 모습과 2008년 3월의 경기 침체로 매출이 굉장히 작았던 모습을 알 수 있다.
ggseasonplot(a10, polar = TRUE) +
ylab("$ Million") +
xlab("Month") +
ggtitle("Seasonal Graph : Antidibiatic drug sales")
극좌표(polar coodinate)를 사용하면 마치 등고선 모양처럼 시각화하여 볼 수 있다. polar=True로 두면 수평축 대신 원형축으로 나타난다.
2.5 계절성 부시계열 그래프
계절성 패턴을 강조하여 시각화하는 방법 중 다른 방법은 각 계절에 대한 데이터를 모아서 분리된 작은 시간 그래프로 나타내는 것이다.
ggsubseriesplot(a10) +
ylab("$ Million") +
xlab("Month") +
ggtitle("Seasonal Graph : Antidibiatic drug sales")
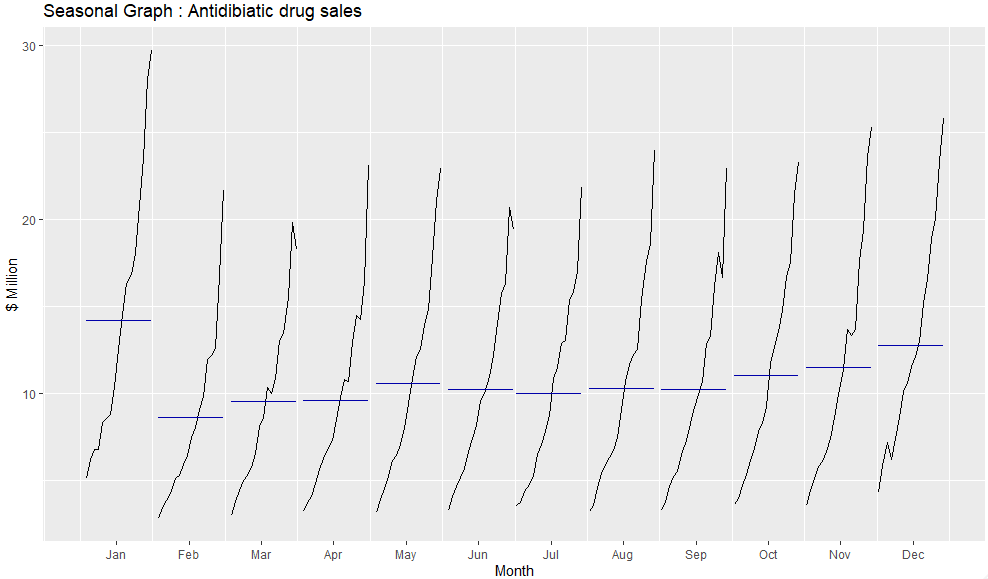
수평선은 각 월에 대한 평균값을 의미하며, 이러한 형태로 중요한 계절성 패턴을 분명히 파악할 수 있다.
2.6 산점도
지금까지의 그래프는 시계열을 시각화하거나 시계열 사이의 관계를 살피는 데 유용하다.
autoplot(elecdemand[,c("Demand","Temperature")], facets=TRUE) +
xlab("Year: 2014") + ylab("") +
ggtitle("Half-hourly electricity demand: Victoria, Australia")
두 시계열은 빅토리아 주 30분단위 전력 수요와 기온이다.
qplot(Temperature, Demand, data=as.data.frame(elecdemand)) +
ylab("Demand (GW)") + xlab("Temperature (Celsius)")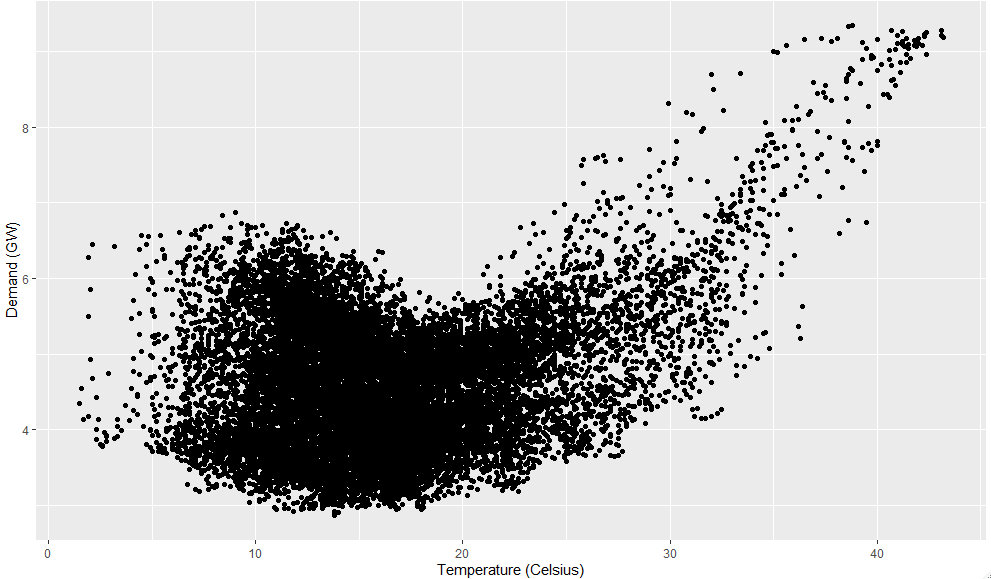
산점도(scatterplot) 는 이러한 변수 사이의 관계를 시각화하는 데 도움이 된다.
상관
상관계수(correlation coefficient)는 두 변수 사이의 관계의 강도를 측정할 때 계산하는 양이다. 두 변수 x와 y 사이의 상관계수는 아래와 같이 주어진다.

r은 항상 -1과 1 사이의 값을 가지며, 음수는 음의 관계를 양수는 양의 관계를 의미한다.

상관계수(correlation coefficient)는 선형관계의 강도만 측정하기 때는데, 종종 데이터를 오해석하는 경우가 생긴다. 상관계수보다 비선형 관계가 더 큰 경우도 있다.

위 그림에서 나오는 상관계수는 모두 같은 값(0.82)이지만 나타나내는 형태는 모두 다르기 때문에, 상관계수의 값에만 의존하기 보다는 데이터를 그려 보는 것이 훨씬 중요하다.
산점도행렬
여러가지 후보의 예측변수(predictor variable)가 있을 때, 각 변수를 다른 변수에 대해 어떤 관계에 있는지 나타내는 것 또한 데이터를 보는 데 도움이 된다.
autoplot(visnights[,1:5], facets=TRUE) +
ylab("Number of visitor nights each quarter (millions)")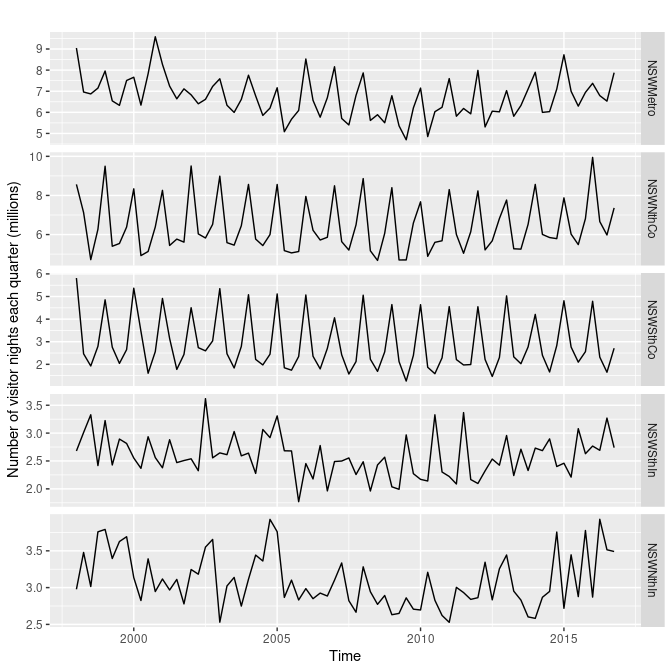
이처럼 여러가지 요소들과 함께 시계열 데이터를 나열하여 나타내서 확인할 수 있다.
2.7 시차 그래프
beer2 <- window(ausbeer, start=1992)
gglagplot(beer2)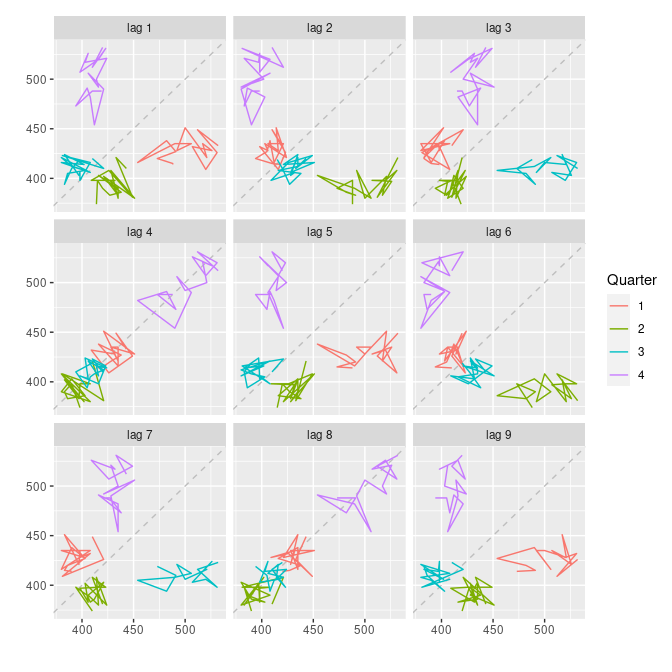
분기별 맥주 생산량에 대한 시차 산점도이다. window() 메서드는 시계열의 부분을 뽑아내는 함수이다.
가로축은 시계열의 시차값(lagged value)를 나타낸다. 그래프는 서로 다른 k값에 대하여 세로축을 가로축에 대해 나타낸 것이다. 세로축의 색상은 분기별 변수를 나타낸다. lag 4, lag 8에서 발견할 수 있는 양의 관계는 데이터에 강한 계절성이 있다는 것을 반영한다. lag 2, lag 6 에서는 음의 관계가 나타난다.
2.8 자기상관
상관값이 두 변수 사이의 선형 관계의 크기를 측정하는 것처럼, 자기상관(autocorrelation)은 시계열의 시차 값(lagged value) 사이의 선형 관계를 측정한다.
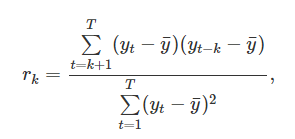
여기서 T는 시계열의 길이이다.

이 값은 산점도와 대응대는 자기상관계수인데, 보통 자기상관함수(ACF)를 나타나기 위해 필요한 값이다.
ggAcf(beer2)
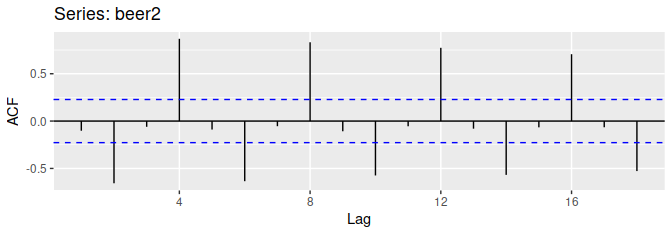
파란 점선은 상관계수가 0과 유의하게 다른지 아닌지를 나타낸다.
ACF 그래프에서 추세와 계절성
데이터에 추세가 존재할 때, 작은 크기의 시차에 대한 자기상관은 큰 양의 값을 갖는 경향이 있는데, 시간적으로 가까운 관측치들이 관측값의 크기에 있어서도 비슷하기 때문이다. 그래서 추세가 있는 시계열의 ACF는 양의 값을 갖는 경향이 크며, 이러한 ACF의 값은 시차가 증가함에 따라 서서히 감소한다.
'개발 > Data Science' 카테고리의 다른 글
| [시계열] 시계열의 개요와 역사 (0) | 2022.09.14 |
|---|---|
| Forecasting : 시계열 회귀 모델(수정중) (0) | 2022.02.24 |
| Forecasting : 판단 예측 (0) | 2022.02.19 |
| Forecasting : 예측가의 도구 상자 (0) | 2022.02.12 |
| Forecasting : 예측이란? 예측에 대한 기초 (0) | 2022.01.28 |




